FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
[EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
, + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI
- X
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Densidade de energia é a quantidade de energia armazenada em um determinado sistema ou região de espaço por unidade de volume . Coloquialmente, também pode ser usado para energia por unidade de massa , embora o termo exato para isso seja energia específica . Frequentemente, apenas a energia útil ou extraível é medida, ou seja, a energia inacessível (como a energia da massa em repouso ) é ignorada. [1] Em contextos cosmológicos e outros contextos relativísticos gerais , no entanto, as densidades de energia consideradas são aquelas que correspondem aos elementos do tensor energia-estressee, portanto, incluem energia de massa e densidades de energia associadas às pressões descritas no próximo parágrafo.
A energia por unidade de volume tem as mesmas unidades físicas que a pressão e, em muitas circunstâncias, é sinônimo : por exemplo, a densidade de energia de um campo magnético pode ser expressa como (e se comporta como) uma pressão física e a energia necessária para comprimir uma um pouco mais de gás comprimido pode ser determinado multiplicando a diferença entre a pressão do gás e a pressão externa pela mudança de volume. Em suma, pressão é uma medida da entalpia por unidade de volume de um sistema. Um gradiente de pressão tem o potencial de realizar trabalho nos arredores, convertendo a entalpia em trabalho até que o equilíbrio seja alcançado.
Introdução à densidade de energia [ editar ]
Existem diferentes tipos de energia armazenados nos materiais, e é necessário um tipo específico de reação para liberar cada tipo de energia. Em ordem da magnitude típica da energia liberada, esses tipos de reações são: nuclear, química, eletroquímica e elétrica.
As reações nucleares ocorrem em estrelas e usinas nucleares, as quais derivam energia da energia de ligação dos núcleos. As reações químicas são usadas pelos animais para obter energia dos alimentos e pelos automóveis para obter energia da gasolina. Os hidrocarbonetos líquidos (combustíveis como gasolina, diesel e querosene) são hoje a maneira mais densa conhecida de armazenar e transportar economicamente energia química em uma escala muito grande (1 kg de diesel queima com o oxigênio contido em ~ 15 kg de ar). As reações eletroquímicas são usadas pela maioria dos dispositivos móveis, como laptops e telefones celulares, para liberar a energia das baterias.
Tipos de conteúdo de energia [ editar ]
Existem vários tipos diferentes de conteúdo de energia. Uma é a quantidade total teórica de trabalho termodinâmico que pode ser derivado de um sistema, com uma dada temperatura e pressão para o ambiente. Isso é chamado de exergia . Outra é a quantidade teórica de trabalho que pode ser derivada de reagentes que estão inicialmente à temperatura ambiente e à pressão atmosférica. Isto é dado pela mudança na energia livre padrão de Gibbs . Porém, como fonte de calor ou para uso em um motor térmico , a quantidade relevante é a alteração na entalpia padrão ou o calor da combustão .
Existem dois tipos de calor de combustão:
- O valor mais alto (HHV), ou calor bruto de combustão, inclui todo o calor liberado à medida que os produtos esfriam à temperatura ambiente e qualquer vapor de água presente se condensa.
- O valor mais baixo (LHV), ou calor líquido de combustão, não inclui o calor que pode ser liberado pelo vapor de água de condensação e pode não incluir o calor liberado no resfriamento até a temperatura ambiente.
Uma tabela conveniente de HHV e LHV de alguns combustíveis pode ser encontrada nas referências. [2]
Densidade de energia em armazenamento de energia e em combustível [ editar ]
Em aplicações de armazenamento de energia, a densidade de energia relaciona a energia em um estoque de energia com o volume da instalação de armazenamento, por exemplo, o tanque de combustível . Quanto maior a densidade de energia do combustível, mais energia pode ser armazenada ou transportada para a mesma quantidade de volume. A densidade de energia de um combustível por unidade de massa é chamada de energia específica desse combustível. Em geral, um motor que utiliza esse combustível gera menos energia cinética devido a ineficiências e considerações termodinâmicas - portanto, o consumo específico de combustível de um motor sempre será maior que a taxa de produção da energia cinética do movimento.
Amplas implicações [ editar ]
A densidade de energia difere da eficiência de conversão de energia (produção líquida por insumo) ou energia incorporada (os custos de produção de energia para fornecer, como colheita , refino , distribuição e tratamento da poluição, todos usam energia). O uso intensivo de energia em grande escala afeta e é impactado pelo clima , armazenamento de resíduos e consequências ambientais .
Nenhum método de armazenamento de energia única ostenta o melhor em potência específica , energia específica e densidade de energia. A Lei de Peukert descreve como a quantidade de energia útil que pode ser obtida (para uma célula de chumbo-ácido) depende da rapidez com que é retirada. Para maximizar a energia específica e a densidade de energia, é possível calcular a densidade de energia específica de uma substância multiplicando os dois valores, onde quanto maior o número, melhor a substância armazenando energia com eficiência.
Opções alternativas são discutidas para o armazenamento de energia para aumentar a densidade de energia e diminuir o tempo de carregamento. [11] [12] [13] [14]
Densidade de energia gravimétrica e volumétrica de alguns combustíveis e tecnologias de armazenamento (modificadas no artigo Gasolina ):
- Nota: Alguns valores podem não ser precisos devido a isômeros ou outras irregularidades. Consulte Valor do aquecimento para obter uma tabela abrangente de energias específicas de combustíveis importantes.
- Nota: Também é importante perceber que geralmente os valores de densidade para combustíveis químicos não incluem o peso do oxigênio necessário para a combustão. Normalmente, são dois átomos de oxigênio por átomo de carbono e um por dois átomos de hidrogênio. O peso atômicode carbono e oxigênio são semelhantes, enquanto o hidrogênio é muito mais leve que o oxigênio. Os números são apresentados desta maneira para os combustíveis em que, na prática, o ar seria atraído apenas localmente para o queimador. Isso explica a densidade energética aparentemente mais baixa dos materiais que já incluem seu próprio oxidante (como pólvora e TNT), onde a massa do oxidante efetivamente adiciona peso morto e absorve parte da energia da combustão para dissociar e liberar oxigênio para continuar a reação. Isso também explica algumas anomalias aparentes, como a densidade de energia de um sanduíche que parece ser maior do que a de um dinamite.
Tabelas de conteúdo energético [ editar ]
Este artigo ou seção parece se contradizer . ( Abril de 2019 )
|
Salvo indicação em contrário, os valores na tabela a seguir são valores mais baixos de aquecimento para uma combustão perfeita, sem contar a massa ou o volume do oxidante. As seguintes conversões de unidade podem ser úteis ao considerar os dados na tabela: 3,6 MJ = 1 kW⋅h ≈ 1,34 hp⋅h .
| Tipo de armazenamento | Energia específica (MJ / kg) | Densidade de energia (MJ / L) | Energia específica ( W⋅h / kg ) | Densidade de energia (W⋅h / L) | Como a energia é liberada e Comentários |
|---|---|---|---|---|---|
| Antimatéria | 89.875.517.874 | Depende da densidade da forma da antimatéria | 24.965.421.631.578 | Depende da densidade da forma da antimatéria | Aniquilação, contando tanto a massa de antimatéria consumida quanto a massa de matéria comum |
| Deutério | 87.900.000 [15] | 15.822 [16] | Reator de fusão (experimental) | ||
| Plutônio-239 | 83.610.000 | 1.300.000.000–1.700.000.000 (Depende da fase cristalográfica ) | 23.222.915.000 | 370.000.000.000–460.000.000.000 (Depende da fase cristalográfica ) | Calor liberado na explosão |
| Plutônio-239 | 31.000.000 | 490.000.000–620.000.000 (depende da fase cristalográfica ) | 8.700.000.000 | 140.000.000.000-170.000.000.000 (Depende da fase cristalográfica ) | Eletricidade produzida no reator de fissão |
| Urânio | 80.620.000 [17] | 1.539.842.000 | 22.394.000.000 | Eletricidade produzida no reator reprodutor | |
| Tório | 79.420.000 [17] | 929.214.000 | 22.061.000.000 | Reator reprodutor (experimental) | |
| Plutônio-238 | 2.239.000 | 43.277.631 | 621.900.000 | RTG | |
| Hidrogênio líquido [18] | 141,86 ( HHV ) 119,93 ( LHV ) | 10,044 (HHV) 8,491 (LHV) | 39.405,6 (HHV) 33.313,9 (LHV) | 2.790,0 (HHV) 2.358,6 (LHV) | Os valores de energia são aplicados após o aquecimento a 25 ° C. |
| Hidrogênio, a 690 bar e 25 ° C [18] | 141,86 (HHV) 119,93 (LHV ) | 5.323 (HHV) 4.500 (LHV) | 39.405,6 (HHV) 33.313,9 (LHV) | 1.478,6 (HHV) 1.250,0 (LHV) | |
| Hidrogênio, gás , 1 atm , 25 ° C [18] | 141,86 (HHV) 119,93 (LHV ) | 0,01188 (HHV) 0,01005 (LHV) | 39.405,6 (HHV) 33.313,9 (LHV) | 3,3 (HHV) 2,8 (LHV) | |
| Diborano [19] | 78,2 | 21.722,2 | |||
| Berílio | 67,6 | 125,1 | 18.777,8 | 34.750,0 | |
| Boro-hidreto de lítio | 65,2 | 43,4 | 18.111,1 | 12.055,6 | |
| Boro [20] | 58,9 | 137,8 | 16.361,1 | 38.277,8 | |
| Metano (1,013 bar, 15 ° C) | 55,6 | 0,0378 | 15.444,5 | 10,5 | |
| GNL (GN a -160 ° C) | 53,6 [21] | 22,2 | 14.888,9 | 6.166,7 | |
| GNC (GN comprimido a 250 bar / ~ 3.600 psi) | 53,6 [21] | 9 | 14.888,9 | 2.500,0 | |
| Gás natural | 53,6 [21] | 0,0364 | 14.888,9 | 10.1 | |
| LPG propano [22] | 49,6 | 25,3 | 13.777,8 | 7.027,8 | |
| Butano a GPL [22] | 49,1 | 27,7 | 13.638,9 | 7.694,5 | |
| Gasolina (gasolina) [22] | 46,4 | 34,2 | 12.888,9 | 9.500,0 | |
| Plástico de polipropileno | 46,4 [23] | 41,7 | 12.888,9 | 11.583,3 | |
| Plástico de polietileno | 46,3 [23] | 42,6 | 12.861,1 | 11.833,3 | |
| Óleo de aquecimento residencial [22] | 46,2 | 37,3 | 12.833,3 | 10.361,1 | |
| Combustível diesel [22] | 45,6 | 38,6 | 12.666,7 | 10.722,2 | |
| 100LL Avgas | 44,0 [24] | 31,59 | 12.222,2 | 8.775,0 | |
| Combustível de avião | 43 [25] [26] [27] | 35 | Motor de avião | ||
| Gasóleo E10 (10% de etanol e 90% de gasolina em volume) | 43,54 | 33.18 | 12.094,5 | 9.216,7 | |
| Lítio | 43,1 | 23,0 | 11.972,2 | 6.388,9 | |
| Óleo de biodiesel (óleo vegetal) | 42,20 | 33 | 11.722,2 | 9.166,7 | |
| DMF (2,5-dimetilfurano) [ esclarecimentos necessários ] | 42 [28] | 37,8 | 11.666,7 | 10.500,0 | |
| Petróleo bruto (de acordo com a definição de tonelada de equivalente petróleo ) | 41.868 | 37 [21] | 11.630 | 10.278 | |
| Plástico de poliestireno | 41,4 [23] | 43,5 | 11.500,0 | 12.083,3 | |
| Corpo gordo | 38. | 35 | 10.555,6 | 9.722,2 | Metabolismo no corpo humano (22% de eficiência [29] ) |
| Butanol | 36,6 | 29,2 | 10.166,7 | 8.111,1 | |
| Gasóleo E85 (85% etanol e 15% gasolina em volume) | 33.1 | 25,65 [ citação necessária ] | 9.194,5 | 7.125,0 | |
| Grafite | 32,7 | 72,9 | 9.083,3 | 20.250,0 | |
| Carvão , antracite [30] | 26-33 | 34-43 | 7.222,2-9.166,7 | 9.444,5–11.944,5 | Os números representam uma combustão perfeita sem contar o oxidante, mas a eficiência da conversão em eletricidade é de ~ 36% |
| Silício [31] [ citação necessário ] | 32,2 | 75,1 | 8.944,5 | 20.861,1 | |
| Alumínio | 31,0 | 83,8 | 8.611,1 | 23.277,8 | |
| Etanol | 30 | 24 | 8.333,3 | 6.666,7 | |
| DME [32] [33] | 31,7 (HHV) 28,4 (LHV) | 21,24 (HHV) 19,03 (LHV) | 8.805,6 (HHV) 7.888,9 (LHV) | 5.900,0 (HHV) 5.286,1 (LHV) | |
| Poliéster plástico | 26,0 [23] | 35,6 | 7.222,2 | 9.888,9 | |
| Magnésio | 24,7 | 43,0 | 6.861,1 | 11.944,5 | |
| Carvão , betuminoso [30] | 24-35 | 26-49 | 6.666,7-9.722,2 | 7.222,2-13.611,1 | |
| Plástico PET (impuro) | 23,5 [34] | 6.527,8 | |||
| Metanol | 19,7 | 15,6 | 5.472,2 | 4,333,3 | |
| Hidrazina (queimado para N 2 + H 2 O) | 19,5 | 19,3 | 5.416,7 | 5.361,1 | |
| Líquido amónia (queimado para N 2 + H 2 O) | 18,6 | 11,5 | 5.166,7 | 3.194,5 | |
| Plástico PVC ( combustão incorreta tóxica ) [ esclarecimentos necessários ] | 18,0 [23] | 25,2 | 5.000,0 | 7.000,0 | |
| Madeira [35] | 18,0 | 5.000,0 | |||
| Briquete de turfa [36] | 17,7 | 4.916,7 | |||
| Açúcares, carboidratos e proteínas [ citação necessária ] | 17 | 26,2 ( dextrose ) | 4.722,2 | 7.277,8 | Metabolismo no corpo humano (22% de eficiência [37] ) |
| Cálcio [ citação necessária ] | 15,9 | 24,6 | 4.416,7 | 6.833,3 | |
| Glicose | 15,55 | 23,9 | 4.319,5 | 6.638,9 | |
| Estrume de vaca seca e estrume de camelo | 15,5 [38] | 4.305,6 | |||
| Carvão , linhito [ citação necessário ] | 10-20 | 2.777,8-5.555,6 | |||
| Sódio | 13,3 | 12,8 | 3.694,5 | 3.555,6 | queimado a hidróxido de sódio molhado |
| Turfa | 12,8 | 3.555,6 | |||
| Nitrometano | 11,3 | 3.138,9 | |||
| Enxofre | 9,23 | 19.11 | 2.563,9 | 5.308,3 | queimado em dióxido de enxofre [39] |
| Sódio | 9.1 | 8,8 | 2.527,8 | 2.444,5 | queimado para secar óxido de sódio |
| Bateria recarregável a ar de lítio | 9,0 [40] | 2.500,0 | Descarga elétrica controlada | ||
| Lixo doméstico | 8,0 [41] | 2.222,2 | |||
| Zinco | 5.3 | 38,0 | 1.472,2 | 10.555,6 | |
| Ferro | 5.2. | 40,68 | 1.444,5 | 11.300,0 | queimado em óxido de ferro (III) |
| Teflon plástico | 5.1 | 11,2 | 1.416,7 | 3.111,1 | combustão tóxica, mas retardante de chamas |
| Ferro | 4.9 | 38,2 | 1.361,1 | 10.611,1 | queimado em óxido de ferro (II) |
| Pólvora | 4,7-11,3 [42] | 5,9-12,9 | |||
| TNT | 4,184 | 6,92 | |||
| ANFO | 3.7 | 1.027,8 | |||
| Bateria de zinco-ar [43] | 1,59 | 6.02 | 441,7 | 1.672,2 | Descarga elétrica controlada |
| Nitrogênio líquido [é necessário esclarecimento ] | 0,77 [44] | 0,62 | 213,9 | 172,2 | |
| Bateria de enxofre de sódio | 0,54-0,86 | 150-240 [45] | |||
| Ar comprimido a 300 bar | 0,5 | 0,2 | 138,9 | 55,6 | Energia potencial |
| Calor latente de fusão de gelo [ citação necessária ] (térmica) | 0,335 | 0,335 | 93,1 | 93,1 | |
| Bateria de metal de lítio | 1.8 | 4,32 | Descarga elétrica controlada | ||
| Bateria de iões de lítio | 0,36-0,875 [48] | 0,9-2,63 | 100.00–243.06 | 250,00–730,56 | Descarga elétrica controlada |
| Volante | 0,36-0,5 | 5.3 | Energia potencial | ||
| Bateria alcalina | 0,48 [49] | 1,3 [50] | Descarga elétrica controlada | ||
| Bateria de hidreto de metal níquel | 0,41 [51] | 0,504-1,46 [51] | Descarga elétrica controlada | ||
| Bateria de chumbo ácido | 0,17 | 0,56 | Descarga elétrica controlada | ||
| Supercapacitor ( EDLC ) | 0,01-0,036 [58] | 0,05-0,06 [59] | Descarga elétrica controlada | ||
| Água a 100 m de altura da barragem | 0.000981 | 0.000978 | 0,272 | 0,272 | Os números representam energia potencial, mas a eficiência da conversão em eletricidade é de 85 a 90% [60] [61] |
| Capacitor eletrolítico | 0,00001-0,0002 [62] | 0,00001-0,001 [65] | Descarga elétrica controlada | ||
| Tipo de armazenamento | Densidade energética em massa (MJ / kg) | Densidade energética em volume (MJ / L) | Energia específica (W⋅h / kg) | Densidade de energia (W⋅h / L) | Como a energia é liberada e Comentários |
x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
A capacidade de armazenamento de energia mecânica, ou resiliência , de um material Hookean quando é deformado até o ponto de falha pode ser calculada calculando-se a resistência à tração vezes o alongamento máximo dividido por dois. O alongamento máximo de um material Hookean pode ser calculado dividindo a rigidez desse material pela sua resistência à tração final. A tabela a seguir lista esses valores calculados usando o módulo de Young como medida de rigidez:
| Material | Densidade de energia em massa
(J / kg)
| Resiliência : densidade de energia em volume
(J / L)
| Densidade
(kg / L)
| Módulo de Young
(GPa)
| Resistência à tração final
(MPa)
|
|---|---|---|---|---|---|
| Plástico ABS | 241-534 | 258-571 | 1.07 | 1,4-3,1 [66] | 40 [66] |
| Acetals | 908 | 754 | 0,831 [67] | 2,8 [66] | 65 [66] |
| Acrílico | 3,2 [66] | 70 [66] | |||
| Alumínio (não ligado) | 32,5 | 87,7 | 2,70 [68] | 69 [66] | 110 [66] |
| Alumínio 7077-T8 (rendimento) | 399 | 1120 [69] | 2,81 [70] | 71,0 [69] | 400 (rendimento) [69] |
| Latão | 28,6-36,5 | 250-306 | 8,4-8,73 [71] | 102-125 [66] | 250 [66] |
| Cobre | 23.1 | 207 | 8,93 [71] | 117 [66] | 220 [66] |
| Berílio de cobre 25-1 / 2 HT (rendimento) | 684 | 5.720 [69] | 8,36 [72] | 131 [69] | 1.224 (rendimento) [69] |
| Resinas epóxi | 113-1810 | 2–3 [66] | 26-85 [66] | ||
| Douglas fir Wood | 158–200 | 96 | .481 - .609 [73] | 13 [66] | 50 (compressão) [66] |
| Vidro | 5,56-10,0 | 13,9–25,0 | 2,5 [74] | 50-90 [66] | 50 (compressão) [66] |
| Nylon-6 | 233-1.870 | 253-230 | 1.084 | 2–4 [66] | 45-90 [66] |
| Pinho (branco oriental americano, flexural ) | 31,8-32,8 | 11,1-11,5 | 0,350 [75] | 8,30–8,56 (flexural) [75] | 41,4 (rendimento à flexão) [75] |
| Policarbonatos | 433-615 | 520-740 | 1,2 [76] | 2,6 [66] | 52-62 [66] |
| Aço, ASTM A228 (rendimento, 1 mm de diâmetro) | 1.440-1.770 | 11.200 - 13.800 | 7,80 [77] | 210 [77] | 2.170–2.410 (rendimento) [77] |
| Aço inoxidável 301-H (rendimento) | 301 | 2.410 [69] | 8,0 [78] | 193 [69] | 965 [69] |
Tabela sobre o conteúdo energético das baterias:
| Dispositivo de armazenamento | Conteúdo energético ( Joule ) | Tipo de energia | Massa típica (g) | Dimensões típicas (diâmetro × altura em mm) | Volume típico em L | Densidade energética em volume (MJ / L) | Densidade energética em massa (MJ / kg) |
|---|---|---|---|---|---|---|---|
| Bateria alcalina AA [79] | 9.360 | Eletroquímico | 24 | 14.2 × 50 | 0,0022 | 0,45 | 0,39 |
| Bateria alcalina C [79] | 34.416 | Eletroquímico | 65 | 26 × 46 | 0,0036 | 0,956 | 0,53 |
| Bateria NiMH AA | 9.072 | Eletroquímico | 26 | 14.2 × 50 | 0,0027 | 0,346 | 0,35 |
| Bateria NiMH C | 19.440 | Eletroquímico | 82 | 26 × 46 | 0,0038 | 0,512 | 0,24 |
| Bateria de íon de lítio 18650 | 28.800–46.800 | Eletroquímico | 44-49 [80] | 18 × 65 | 0,0037 | 0,778–1,27 | 0,59–1,06 |
x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Fontes de energia nucleares [ editar ]
A maior fonte de energia, de longe, é a própria massa. Essa energia, E = mc 2 , onde m = ρV , ρ é a massa por unidade de volume, V é o volume da massa em si ec é a velocidade da luz. Essa energia, no entanto, pode ser liberada apenas pelos processos de fissão nuclear (0,1%), fusão nuclear (1%) ou aniquilação de parte ou de toda a matéria no volume V por colisões matéria-antimatéria (100%) . [ citação necessária ]As reações nucleares não podem ser realizadas por reações químicas, como a combustão. Embora maiores densidades de matéria possam ser alcançadas, a densidade de uma estrela de nêutrons se aproximaria do sistema mais denso capaz de aniquilação de matéria-antimatéria possível. Um buraco negro , embora mais denso que uma estrela de nêutrons, não possui uma forma antipartícula equivalente, mas ofereceria a mesma taxa de conversão de 100% da massa em energia na forma de radiação Hawking. No caso de buracos negros relativamente pequenos (menores que objetos astronômicos), a potência seria tremenda.
As fontes de energia de maior densidade, além da antimatéria, são a fusão e a fissão . A fusão inclui energia do sol, que estará disponível por bilhões de anos (na forma de luz solar), mas até agora (2018), a produção sustentada de energia de fusão continua a ser ilusória.
A energia da fissão de urânio e tório em usinas nucleares estará disponível por muitas décadas ou mesmo séculos, devido ao suprimento abundante de elementos na Terra, [81] embora o potencial total dessa fonte só possa ser realizado por reatores de reprodução , que além do reator BN-600 , ainda não são utilizados comercialmente. [82] Carvão , gás e petróleo são as fontes de energia primária atuais nos EUA [83], mas possuem uma densidade energética muito menor. A queima de combustíveis locais de biomassa fornece as necessidades de energia das famílias ( cozinhas , lâmpadas de óleoetc.) em todo o mundo.
A energia térmica dos reatores de fissão nuclear [ editar ]
A densidade de energia térmica contida no núcleo de um reator de água leve ( PWR ou BWR ) de tipicamente 1 GWe (1.000 MW elétricos correspondentes a ~ 3.000 MW térmicos) está na faixa de 10 a 100 MW de energia térmica por cúbico metro de água de resfriamento, dependendo da localização considerada no sistema (o próprio núcleo (~ 30 m 3 ), o vaso de pressão do reator (~ 50 m 3 ) ou todo o circuito primário (~ 300 m 3 )). Isso representa uma densidade considerável de energia que requer, em todas as circunstâncias, um fluxo contínuo de água em alta velocidade para poder remover o calordo núcleo, mesmo após um desligamento de emergência do reator. A incapacidade de resfriar os núcleos de três reatores de água fervente (BWR) em Fukushima em 2011 após o tsunami e a perda resultante da energia elétrica externa e da fonte de frio foram a causa do colapso dos três núcleos em apenas algumas horas , mesmo que os três reatores tenham sido desligados corretamente logo após o terremoto de Tōhoku . Essa densidade de energia extremamente alta distingue usinas nucleares (centrais nucleares) de quaisquer usinas termelétricas (queima de carvão, combustível ou gás) ou quaisquer usinas químicas e explica a grande redundância necessária para controlar permanentemente a reatividade de nêutrons e remover o calor residual do núcleo NPP's.
Densidade de energia de campos elétricos e magnéticos [ editar ]
Campos elétricos e magnéticos armazenam energia. No vácuo, a densidade de energia (volumétrica) é dada por
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
onde E é o campo elétrico e B é o campo magnético . A solução será (em unidades SI) em Joules por metro cúbico. No contexto da magneto-hidrodinâmica , a física dos fluidos condutores, a densidade da energia magnética se comporta como uma pressão adicional que aumenta a pressão do gás no plasma .
Em substâncias normais (lineares e não dispersivas), a densidade de energia (em unidades SI) é
- x
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
No caso de ausência de campos magnéticos, explorando as relações de Fröhlich, também é possível estender essas equações para dielétricos de anisotropia e não linearidade , bem como calcular as densidades correlacionadas de energia e entropia de Helmholtz . [84]
Quando um laser pulsado afeta uma superfície, a exposição radiante , ou seja, a energia depositada por unidade de superfície, pode ser chamada densidade ou fluência de energia . [85]
O tensor de tensão Maxwell (nomeado após James Clerk Maxwell ) é um tensor simétrico de segunda ordem usado no eletromagnetismo clássico para representar a interação entre forças eletromagnéticas e momento mecânico . Em situações simples, como uma carga pontual se movendo livremente em um campo magnético homogêneo, é fácil calcular as forças sobre a carga a partir da lei de forças de Lorentz . Quando a situação se torna mais complicada, esse procedimento comum pode se tornar impossivelmente difícil, com equações que abrangem várias linhas. Portanto, é conveniente coletar muitos desses termos no tensor de tensão Maxwell e usar a aritmética do tensor para encontrar a resposta para o problema em questão.
Na formulação relativística do eletromagnetismo, o tensor de Maxwell aparece como parte do tensor eletromagnético de tensão-energia, que é o componente eletromagnético do tensor total de tensão-energia . Este último descreve a densidade e o fluxo de energia e momento no espaço-tempo .
Motivação [ editar ]
Como descrito em seguida, a força electromagnética é escrita em termos de E e B . Usando o cálculo vetorial e as equações de Maxwell , busca-se simetria nos termos que contêm E e B , e a introdução do tensor de tensão Maxwell simplifica o resultado.
Equações de Maxwell em unidades SI no vácuo
(para referência)Nome Forma diferencial Lei de Gauss (no vácuo) Lei de Gauss para o magnetismo Equação de Maxwell – Faraday
(lei de indução de Faraday)Lei circuital de Ampère (no vácuo)
(com correção de Maxwell)- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
- Começando com a lei da força de Lorentz
- X
- V
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
a força por unidade de volume é - Em seguida, ρ e J podem ser substituídos pelos campos E e B , usando a lei de Gauss e a lei circuital de Ampère :
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
- A derivada do tempo pode ser reescrita para algo que possa ser interpretado fisicamente, a saber, o vetor de Poynting . O uso da regra do produto e da lei de indução de Faraday fornecee agora podemos reescrever f comoentão coletar termos com E e B dá
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
- Um termo parece estar "ausente" da simetria em E e B , o que pode ser alcançado através da inserção de (∇ ⋅ B ) B devido à lei de Gauss para magnetismo :Eliminando os cachos (que são razoavelmente complicados de calcular), usando a identidade de cálculo vetorialleva a:
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Essa expressão contém todos os aspectos do eletromagnetismo e momento e é relativamente fácil de calcular. Pode ser escrito de forma mais compacta, introduzindo o tensor de tensão Maxwell ,Todos, exceto o último termo de f, podem ser escritos como a divergência tensorial do tensor de tensão Maxwell, fornecendo:- ,
Como no teorema de Poynting , o segundo termo no lado direito da equação acima pode ser interpretado como a derivada no tempo da densidade de momento do campo EM, enquanto o primeiro termo é a derivada no tempo da densidade de momento para as partículas maciças. Dessa maneira, a equação acima será a lei da conservação do momento na eletrodinâmica clássica.
na relação acima para conservação do momento, é a densidade do fluxo de momento e desempenha um papel semelhante aono teorema de Poynting .
A derivação acima pressupõe um conhecimento completo de ρ e J (cargas e correntes livres e limitadas). No caso de materiais não lineares (como ferro magnético com curva BH), deve-se usar o tensor de tensão Maxwell não linear. [1]
Equação [ editar ]
Na física , o tensor de tensão Maxwell é o tensor de tensão de um campo eletromagnético . Como derivado acima em unidades SI , é dado por:
- ,
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
onde ε 0 é a constante elétrica e μ 0 é a constante magnética , E é o campo elétrico , B é o campo magnético e δij é o delta de Kronecker . Na unidade gaussiana de cgs , é dada por:
- ,
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Uma maneira alternativa de expressar esse tensor é:
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
O elemento ij do tensor de tensão de Maxwell tem unidades de força por unidade de área por unidade de tempo e dá o fluxo de quantidade de movimento paralelo ao i º eixo atravessando uma superfície normal ao j º eixo (no sentido negativo) por unidade de tempo .
Essas unidades pode também ser visto como unidades de força por unidade de área (pressão negativa), e o ij elemento do tensor também pode ser interpretado como a força paralela ao i º eixo sofrido por uma superfície normal ao j eixo por unidade de área. De fato, os elementos diagonais dão a tensão (tração) atuando em um elemento de área diferencial normal ao eixo correspondente. Ao contrário das forças devido à pressão de um gás ideal, um elemento de área no campo eletromagnético também sente uma força em uma direção que não é normal ao elemento. Esse cisalhamento é dado pelos elementos fora da diagonal do tensor de tensão.
Apenas magnetismo [ editar ]
Se o campo for apenas magnético (o que é amplamente verdadeiro em motores, por exemplo), alguns dos termos desaparecem e a equação nas unidades SI se torna:
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Para objetos cilíndricos, como o rotor de um motor, isso é ainda mais simplificado para:
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
onde r é o cisalhamento na direção radial (para fora do cilindro) e t é o cisalhamento na direção tangencial (ao redor do cilindro). É a força tangencial que gira o motor. B r é a densidade do fluxo na direção radial e B t é a densidade do fluxo na direção tangencial.
Em eletrostática [ editar ]
Em eletrostática, os efeitos do magnetismo não estão presentes. Nesse caso, o campo magnético desaparece,, e obtemos o tensor de tensão eletrostático de Maxwell . É dado em forma de componente por
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
e em forma simbólica por
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Onde é o tensor de identidade apropriado (geralmente )
Valor próprio [ editar ]
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Esses autovalores são obtidos aplicando iterativamente o lema determinante da matriz , em conjunto com a fórmula de Sherman-Morrison .
Observando que a matriz da equação característica, , pode ser escrito como
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Onde
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
montamos
Aplicando o lema determinante da matriz uma vez, isso nos dá
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Aplicá-lo novamente produz,
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Desde o último multiplicando no RHS, vemos imediatamente que é um dos valores próprios.
Para encontrar o inverso de , usamos a fórmula de Sherman-Morrison:
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Factoring out a termo no determinante, resta encontrar os zeros da função racional:
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
Assim, uma vez que resolvemos
- X
FUNÇÃO FUNDAMENTAL E GERAL Do SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EN CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.E DE ESTADOS TRANSICIONAIS
obtemos os outros dois autovalores.
Densidade de energia é a quantidade de energia (taxa de tempo de transferência de energia ) por unidade de volume .
Nos transformadores de energia, incluindo baterias , células de combustível , motores, etc., e também unidades de fornecimento de energia ou similares, a densidade de energia refere-se a um volume. É então também chamado de densidade de potência de volume , que é expressa em W / m 3 .
Às vezes, a densidade de potência do volume é uma consideração importante quando o espaço é limitado.
Nos motores de combustão interna alternativos , a densidade de potência - potência por volume varrido ou potência de freio por centímetro cúbico - é uma métrica importante. Isso se baseia na capacidade interna do mecanismo, não no tamanho externo.
Exemplos [ editar ]
| Material de armazenamento | Tipo de energia | Potência específica (W / kg) | Densidade de potência (W / m 3 ) |
|---|---|---|---|
| Hidrogênio (em estrela) | Fusão estelar | 0,00184 | 276,5 |
| Plutônio | Decaimento alfa | 1,94 | 38.360 |
| Supercapacitores | Capacitância | até 15000 | Variável |
| Íon-lítio | Químico | ~ 250-350 | ~ 700 |
X
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC].
 + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE
 + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL ![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCK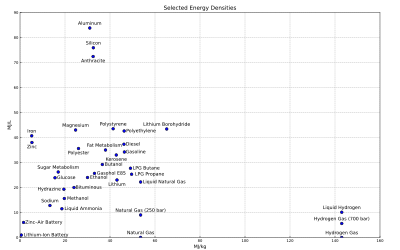












![{\ displaystyle \ mathbf {f.} = \ epsilon _ {0} \ left [({\ boldsymbol {\ nabla}} \ cdot \ mathbf {E}) \ mathbf {E} - \ mathbf {E} \ times ({ \ boldsymbol {\ nabla}} \ times \ mathbf {E}) \ right] + {\ frac {1} {\ mu _ {0}}} \ left [- \ mathbf {B} \ times \ left ({\ símbolo de negrito {\ nabla}} \ times \ mathbf {B} \ right) \ right] - \ epsilon _ {0} {\ frac {\ parcial} {\ t parcial}} \ left (\ mathbf {E} \ times \ mathbf {B} \ right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0372ec4582a8e8e3a7d8cec2ada39b2357b47163)
![{\ displaystyle \ mathbf {f.} = \ epsilon _ {0} \ left [({\ boldsymbol {\ nabla}} \ cdot \ mathbf {E}) \ mathbf {E} - \ mathbf {E} \ times ({ \ boldsymbol {\ nabla}} \ times \ mathbf {E}) \ right] + {\ frac {1} {\ mu _ {0}}} \ left [({\ boldsymbol {\ nabla}} \ cdot \ mathbf {B}) \ mathbf {B} - \ mathbf {B} \ times \ left ({\ boldsymbol {\ nabla}} \ times \ mathbf {B} \ right) \ right] - \ epsilon _ {0} {\ frac {\ parcial} {\ parcial t}} \ esquerda (\ mathbf {E} \ times \ mathbf {B} \ right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c43c1d132f419b56d70aebb6857121cc10fb929a)

![{\ displaystyle \ mathbf {f.} = \ epsilon _ {0} \ left [({\ boldsymbol {\ nabla}} \ cdot \ mathbf {E}) \ mathbf {E} + (\ mathbf {E} \ cdot { \ boldsymbol {\ nabla}}) \ mathbf {E} \ right] + {\ frac {1} {\ mu _ {0}}} \ left [({\ boldsymbol {\ nabla}} \ cdot \ mathbf {B }) \ mathbf {B} + (\ mathbf {B} \ cdot {\ boldsymbol {\ nabla}}) \ mathbf {B} \ right] - {\ frac {1} {2}} {\ boldsymbol {\ nabla }} \ left (\ epsilon _ {0} E ^ {2} + {\ frac {1} {\ mu _ {0}}} B ^ {2} \ right) - \ epsilon _ {0} {\ frac {\ parcial} {\ parcial t}} \ esquerda (\ mathbf {E} \ times \ mathbf {B} \ right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/389c4468e67e0924664ab8ae595c2e1a56065b39)







![{\ displaystyle {\ overset {\ leftrightarrow} {\ boldsymbol {\ sigma}}} = {\ frac {1} {4 \ pi}} \ left [\ mathbf {E} \ otimes \ mathbf {E} + \ mathbf {H} \ otimes \ mathbf {H} - {\ frac {E ^ {2} + H ^ {2}} {2}} \ mathbb {I} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc96a687899ade8163f388d7766b1fcfcc27de05)




















